This is a work in progress - I'm still plugging in the numbers
A couple of issues:
You appear to be mixing Force (effort) and Inertia and comparing them directly - this mistake seems to have come from the first link;- You used 8 mm diameter, instead of 4 mm radius, to calculate the torque
- You haven't calculated the holding force, which would provide the holding torque required, which can be easily compared against the specification of the stepper motor;
- I can't see where you obtained the value for axial force of 10 N, from the datasheet of the stepper motor.
Regardless of these issues, tackling each question separately:
Selection stepper motor to lift given weight?
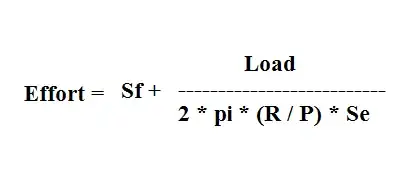
First equation
Your first equation, for effort, is
$$F_{effort} = S_f+\frac{Load}{2*\pi*\left(\frac{R}{P}\right)*S_e}$$
where,
- Starting Force, from linked article, worst case scenario, $S_f = 20$ N
- Radius $R=4$ mm$=0.004$ m
- Pitch $P=1.25$ mm$=0.0125$ m, and
- Screw Efficiency, from linked article, worst case scenario 20 %, $S_e=20=0.2$
So filling in the numbers, for 25 N:
$$effort = 20+\frac{25}{2*\pi*\left(\frac{0.004}{0.00125}\right)*0.2}$$
$$effort = 26.22$$
It is worth noting that this running torque only comes to 6.22 N, much smaller than the worse case value of the starting force, of 20 N:
$$\frac{25}{2*\pi*\left(\frac{0.004}{0.00125}\right)*0.2}$$
$$ = 6.22$$
and plugging in the numbers, for 50 N:
$$effort = 20+\frac{50}{2*\pi*\left(\frac{0.004}{0.00125}\right)*0.2}$$
$$effort = 32.44$$
Again, it is worth noting that this running torque only comes to 12.44 N, much smaller than the worse case value of the starting force, of 20 N:
$$\frac{50}{2*\pi*\left(\frac{0.004}{0.00125}\right)*0.2}$$
$$ = 12.44$$
It should be noted that these values are for a force, in N, not torque, in N•m, and I can't see on the datasheet were you obtained an Axial force of 10 N. To convert these to a torque, you must multiply by the radius of the M8 x 1.25 spindle - M8 is 8 mm, therefore the radius is 4 mm, which is 0.004 m:
$$T_{raise} = F_{effort} \times 0.004$$
Thus reducing the values for the Torque (derived from the effort) even further, by a couple of orders of magnitude, to 0.104 and 0.12976 N•m, for loads of 25 N and 50 N respectively.
So, the estimated value of worst case starting force would appear to be the dominant factor in selecting the stepper motor.
Regardless of all this, if, as you say, that the holding torque, $T_H$, is higher than the running torque, $T_{raise}$, then the holding torque would be the deciding factor in selecting a stepper and the running torque can be discounted.
It is unclear whether the equation that you found is the appropriate equation for calculating the holding torque. This equation appears to be for moving the load, whereas you need it for merely holding the load. For completeness both the holding and lowering torque values should be calculated.
Second equation
Your second equation apparently from Wikipedia - Force, via Lead Screw Torque and Force Calculator,
$$Torque_{raise} = F*D_m/2*\frac{L+\mu*\pi*D_m}{\pi*D_m-\mu*L}$$
where,
- Force, $F$
- Diameter, $D_m$
- Pitch distance of square thread, $L=\frac{1}{D_{Thread}}$, where $D_{Thread}$ is the thread density given in the table.
- Coefficient of friction, $\mu$
Whilst I can not see that equation on Wikipedia's Force page, I did manage to find the equation for raising, and the equation for lowering, on the Wikipedia page for Leadscrews - Mechanics1:
$$T_R = \frac{Fd_m}{2}\left(\frac{l+\pi\mu{d_m}}{\pi{d_m}-\mu{l}}\right)$$
and
$$T_L = \frac{Fd_m}{2}\left(\frac{\pi\mu{d_m}-l}{\pi{d_m}+\mu{l}}\right)$$
Plugging in the numbers for 50 N of load:
$$T_R = \frac{50\times0.007375}{2}\left(\frac{0.00125+\pi\times 0.25\times0.007375}{\pi\times0.007375-0.25\times0.00125}\right)$$
$$T_R = 0.1848 \times 0.308$$
$$T_R = 0.0568$$
Plugging in the numbers for 50 N of load:
$$T_L = \frac{50\times0.007375}{2}\left(\frac{\pi\times 0.25\times0.007375- 0.00125}{\pi\times0.007375+0.25\times0.00125}\right)$$
$$T_L = 0.1848 \times 0.193$$
$$T_L = 0.0357$$
NOTE: As the link to the calculator states, there are two different torques - one to raise, $T_R$, and one to lower, $T_L$. As the lowering torque, $T_L$, is less than the raising torque, $T_R$, then it isn't really necessary to calculate it, or consider it when selecting the stepper, as the raising torque is the dominant factor.
Again, if, as you say, that the holding torque, $T_H$, is higher than the running torque i.e. $T_R$, then the holding torque would be the deciding factor in selecting a stepper and the running toque can be discounted.
Amount of load threaded rod can handle?
This would appear to be much simpler to answer, as a value is given in the specifications for the rod, depending upon what you actually mean. It could be:
- The weight that the rod can support before slipping, or;
- The weight that the rod can support before slipping before mechanical failure,
I would imagine that, the specification given is the weight supported before the threads give way and break.
Footnotes
1 These equations only account for the friction of the thread and the term for the collar appears to have been omitted.
From Torque Required to Raise Load (TR) Calculation, the full equation, for both thread and collar, is given by:
$$T_R = \frac{Fd_m}{2}\left(\frac{l+\pi\mu{d_m}}{\pi{d_m}-\mu{l}}\right)+\left(\frac{F\mu_cd_c}{2}\right)$$
where,
- Torque required to raise load, $T_R$
- Load, $F=50$ N
- Mean diameter of square thread, $d_m = X?$ m
- Mean diameter of collar, $d_c = X?$ m
- Pitch distance of square thread, $l = 0.00125$ m
- Coefficient of friction for thread, taken from the Solved Example, $\mu = 0.25$
- Coefficient of friction of collar, taken from the Solved Example, $\mu_c = 0.25$
As the mean diameter, $d_m$ is not provided, it can be determined from the pitch, $l$, and nominal diameter, $d_n = 8$ mm, by
$$d_m = d_n-\frac{l}{2}$$
$$d_m = 0.008 -\frac{0.00125}{2}$$
$$d_m = 0.007375$$
The mean diameter of collar, $d_c$ is not given...
Plugging in the numbers for 50 N of load:
$$T_R = \frac{50\times0.007375}{2}\left(\frac{0.00125+\pi\times 0.25\times0.007375}{\pi\times0.007375-0.25\times0.00125}\right)+\left(\frac{50\times0.25\times{d_c}}{2}\right)$$
$$T_R = 0.1848 \times 0.308+\left(6.25\times{d_c}\right)$$
$$T_R = 0.0568+\left(6.25\times{d_c}\right)$$